TN 11th, Maths Chapter 1, Exercise 1.4
Welcome To
Class : XISubject : Maths
Chapter : 1
Exercise : 1.4
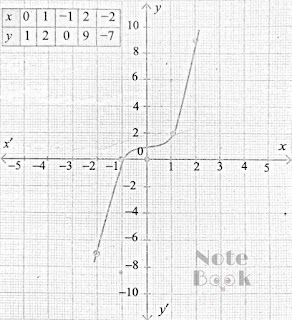
Que 1 :
For the curve y = x³ given in Figure, draw
(i) y = -x³
(ii) y = x³ + 1
(iii) y = x³–1
(iv) y = (x + 1)³, with the same scale.
Solution :
(i) y = -x³
y=-f(x) It is the reflection of the graph of f About the x-axis
(ii) y = x³ + 1
The graph of y = f(x) + 1 is shifted upward to 1 unit.
(iii) y = x³ – 1
The graph of y = x³ – 1 is shifted downward to 1 unit
(iv) y = (x + 1)³
The graph of y = (x + 1)³ is shifted to the left for 1 unit.
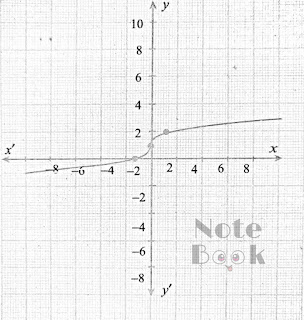
Que 2 :
For the curve, y = (x^⅓) given in figure draw.
(i) y = (-x^⅓)
(ii) y=(x^⅓) +1
(iii) y= (x^⅓) -1
(iv) y=(x+1)^⅓
Solution :
(i) y = (- x)^⅓
Then y = -x^⅓ is the reflection of the graph of y=x^⅓ about the x-axis.
(ii) y=(x^⅓) +1
Then y= (x^⅓)+1 is the x graph of y = x^⅓ shifts to the upwards for one unit.
(iii) y= (x^⅓) -1
Then y = (x^⅓)-1 is the graph of (x^⅓) shifts to the downward for one unit.
(iv) y=(x+1)^⅓
Then y = (x+1)^⅓, it causes the graph of x^⅓, shift to the left for one unit.
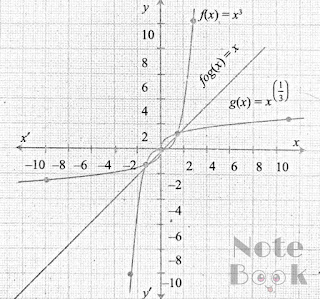
Que 3 :
Graph the functions f(x) = x³ And g(x) = (³√x) on the same coordinate plane. Find fog and graph it on the plane as well. Explain your results.
Solution :
Given functions are f(x) = x³ and g(x) = x⅓.
Now, fog(x) = f(g(x)) = f (x⅓) = (x³)^⅓ = x
Since fog(x) = x is symmetric about the line y=x, g(x) is the inverse of f(x) ∴ g(x) = f-¹(x).
Que 4 :
Write the steps to obtain the graph of the function y = 3(x – 1)²+5 from the graph y = x².
Solution:
Step 1: Draw The Graph Of y = x².
Step 2: The Graph Of y = ( x-1)², shifts to the right for 1 unit.
Step 3: The Graph Of y = 3(x-1)², Compresses towards the y-axis that is moves away from the x-axis since the multiplying factor is 3 Which is greater than 1.
Step 4: The Graph Of y=3(x-1)²+5, causes the shift to the upwards for 5 units.
Que 5 :
From The Curve y = sin x, Graph the functions
(i) y = sin(-x)
(ii) y = -sin(-x)
(iii) y = sin ((π/2) + x) which is cos x
(iv) y = sin ((π/2) – x) which is also cos x (refer trigonometry)
Solution:
Solution :
(i) y = sin(-x)
y=sin(-x) is the reflection of the graph of sim x, about y-axis.
(ii) y = -sin(-x)
y = -sin(-x) is the reflection of y = sin(-x) which is Same as y = sin x.
(iii) y = sin ((π/2) + x) which is cos x
y = sin [(π/2) + x] it causes the shift to the left for (π/2) units.
(iv) y = sin ((π/2) – x) which is also cos x
y = sin [(π/2) - x ] causes the shift to the right for (π/2) unit to the sin(-x) curve.
Que 6 :
From the curve y = x, draw
(i) y = -x
(ii) y = 2x
(iii) y = x + 1
(iv) y = (1/2)x + 1
(v) 2x + y + 3 = 0.2
Solution :
(i) y = -x
Graph of y=(-x) is the reflection of the graph of y=x about the x-axis.
(ii) y = 2x
Graph of y=2x Compresses towards the y-axis that is move away from the x-axis since the multiplying factor is 2, which is greater than 1.
(iii) y = x + 1
The Graph Of y=x+1, causes the shift to the upwards for one unit.
(iv) y = (1/2)x + 1
The graph of y= (1/2)x + 1, stretches towards the X-axis since the multiplying factor 1/2 is which is less than one and shifts to the upward for one unit.
(v) 2x + y + 3 = 0.2
The graph of y = -2x - 3, stretches towards the X-axis since the multiplying factor is - 2 which is less than one and causes the shifts to the downward for 3 units.
Que 7 :
From the curve y = |x|, draw
(i) y= |x – 1| + 1
(ii) y = |x + 1| – 1
(iii) y = |x + 2| – 3.
Solution :
(i) y= |x – 1| + 1
The graph of y=|x - 1|+1, shifts to the right for one unit and causes the shift to the upward for one unit.
(ii) y = |x + 1| – 1
The graph of y = |x + 1|-1, shifts to the left for one unit and causes the shift to the downward for one unit.
(iii) y = |x + 2| – 3
The graph of y =|x + 2|-3, shifts to the left for 2 units and causes the shift to the downward for 3 units.
Que 8 :
From the curve y = sin x, draw y=sin bax! (Hint: sin(x) =-sin x.)
Solution :
We know That
|x| = x if x ≥ 0; -x if x < 0;
∴ sin|x| = sin x if x ≥ 0
and sin |x| = sin (-x) = - sin x if x <0.
The graph of y = sin (-x) =- sinx is the reflection of the graph of sin x about Y- axis.
If Any Doubt Click Here To Contact In WhatsApp
Thank You For Refering On Our Page
























Comments
Post a Comment